Overview
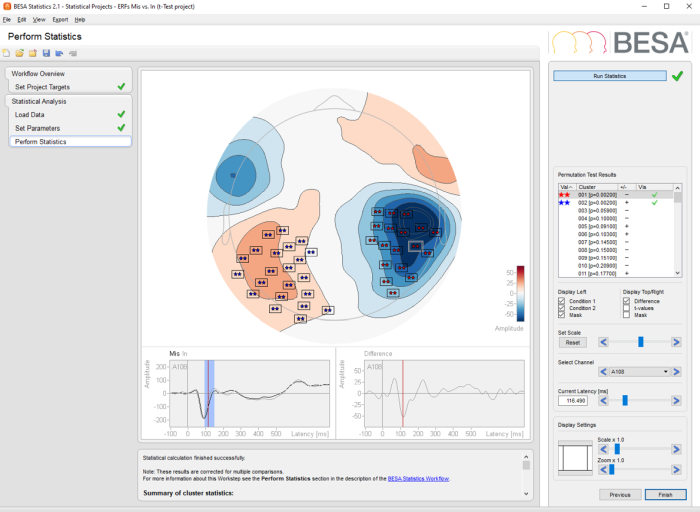
BESA Statistics
BESA Statistics 2.1 greatly enhances the options of the previous version 2.0. As before, dedicated workflows allow you to perform t-test, single-factor ANOVA, and correlation analyses of your data using the parameter-free cluster permutation statistics which so elegantly solve the multiple-test problem. Several new input data types were added to this pipeline, in order to ensure that time-frequency analyses and connectivity analyses are now fully supported.
Highlights of the latest release include
- In all workflows, the data type Connectivity can now be used. This enables direct import of results obtained by BESA Connectivity for group statistics on connectivity results in sensor space or source space.
- For Image data, a configurable slice view is available that displays sequences in one of three available orthogonal orientation.
- The color theme can be adjusted between BESA White and the previous BESA Standard.
- Several new color maps are available.
- The data values are displayed on mouse-over in the detail windows.
- Time-frequency data stored by BESA Connectivity with wavelet analysis can now be read with the correct (logarithmic) frequency spacing.
- Single-trial time-frequency data can now be read in the t-test workflow (*.tfcs data format).
- There is no upper limit on the number of data files imported into the workflow.
- A new image export format is available (svg).
- Screenshots and cluster summary results can now be copied to the clipboard using the right mouse popup menu.
Furthermore, high-DPI displays are supported, exported information was enhanced, and more. Please check the Update History for details.
BESA Statistics provides optimized, user-guided workflows for cross-subject analysis of EEG / MEG data. The statistical method used is parameter-free permutation testing on the basis of Student’s t-tests (Maris, E. and Oostenveld, R., 2007), F-tests (for ANOVA/ANCOVA), and correlations. The program is maximally user-friendly. All analyses are computed automatically with user-interaction minimized to defining time and / or frequency ranges of interest. Statistical values computed in BESA Statistics 2.1 can be directly used for scientific reports. No further analysis in other programs is needed. All results are visualized and can be directly used for publications.
BESA Statistics 2.1 integrates optimally with data that were analyzed in BESA Research, but it can also process data from other software packages as long as they conform to the BESA Statistics file format. The BrainVision Analyzer 2 native data format is supported for time and time-frequency data.
BESA Statistics will automatically identify clusters in time, and if applicable frequency and space where data of the input groups / conditions are not interchangeable, i.e. where the null-hypothesis that all groups / conditions are equal must be rejected. Results are considered corrected for multiple comparisons as only those clusters will be identified that have higher cluster values than 95% of all clusters derived by random permutation of data. Thus, results obtained by BESA Statistics are objective and robust.
For ANOVA/ANCOVA analysis, an additional non-parametric post-hoc Scheffe’s test is computed to determine, which pairwise comparison(s) were responsible for the group / condition main effect. A Bonferroni-Holm correction for multiple comparisons of the different pairwise combinations is applied subsequently.
–>